はじめに
計算式で理解する債券価格と金利の関係
ここで最終利回りと所有期間利回りの計算式を挙げておきましょう。
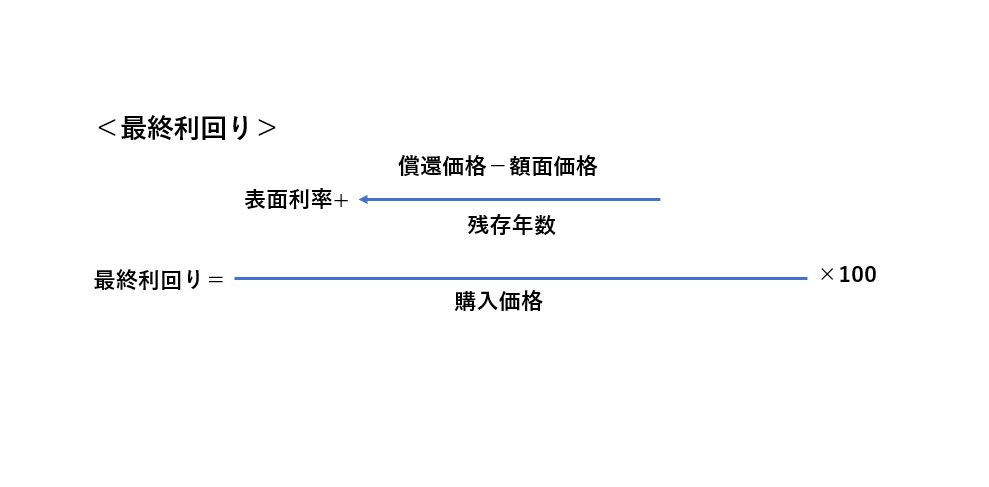
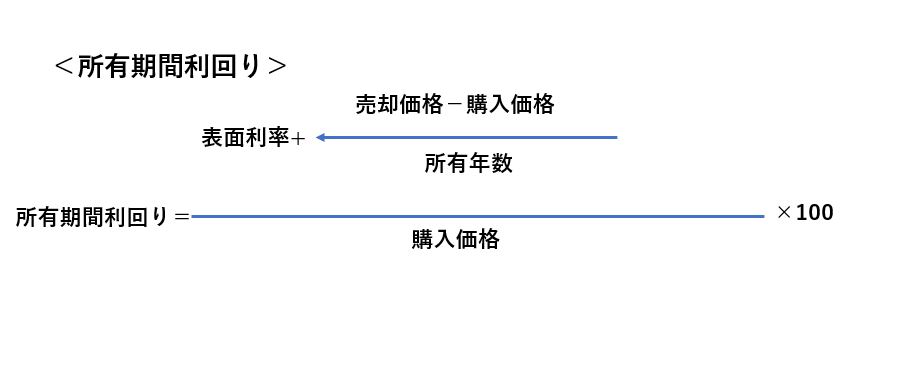
両者を見比べると似たような計算式になるのですが、違う点もあります。それは、最終利回りが償還価格から購入価格を差し引いて、それを残存年数で割るところが、所有期間利回りの場合は、売却価格から購入価格を差し引き、それを所有年数で割るところです。
問題は、所有年数が3年とか5年というように、年でぴったりの場合はそのままの数字を入れれば良いのですが、1年2カ月というように、2カ月間の端数期間が生じている場合です。
この場合は、たとえば端数期間が2カ月なら2カ月÷12か月=0.16になるので、1年2カ月は1.16を入れます。したがって1年6カ月なら1.5ですし、1年9カ月なら1.75を入れます。
以上の計算式を眺めると分かると思いますが、購入時の債券価格が、額面価格もしくは売却価格よりも高くなればなるほど、利回りは低下しますし、それとは逆に、購入時の債券価格が、額面価格もしくは売却価格よりも安くなればなるほど、利回りは上昇します。
よく、債券の特性について、「金利が上昇するほど債券価格は値下がりし、金利が低下するほど債券価格は値上がりする」と言われますが、その特性は、以上の計算式からも理解できると思います。
そのため債券市場では、市場金利の先行き見通しよる値動きを利用して、債券の売買益を狙うトレーディングが、日々繰り返されています。長期金利が時々刻々と変動しているのは、そのためなのです。
