はじめに
中央値、最頻値はいつ使える?
もっと自分の感覚に近い「ふつうの世帯の貯蓄額」を知る方法はないのか−−あります。それが「中央値」です。
中央値を見つけるときは、データを小さい順に並べます(大きい順でも同じ)。81ページの5人の例では、真ん中の3番めの人の身長を「中央値」とみなしますので、170センチです。貯蓄グラフでいうと、中央値は1061万円と書かれています。
中央値1061万円は、平均値の1791万円に比べると半分近く(約60%)まで下がりました。約1000万円というと、まだまだ高く感じますが、世間の人はそれくらいもっているということでしょうか。

上の6人の例では偶数のため、「真ん中」の人がいません。偶数のときは、真ん中2つのデータの平均を「中央値」としますので、165センチです。
もう1つ、「最頻値」という代表値があります。これはデータの中でいちばん多く出てくる(最も頻繁に……から「最頻値」という)データを指すもので、いわば多数決のようなものです。
上の例でいうと、160センチの人が3人いるので、最頻値は160センチです。貯蓄のグラフには最頻値の金額が書かれていませんでしたが、区間で考えると「100万円未満」がいちばん多いので、「最頻値は100万円未満」と判断してもよいでしょう。なお、最頻値は必ずしも1つとは限らず、2つ、3つと出てくることもあります。
どれを「代表値」とするか?
さて、データを代表する値(代表値)を3つ見てきました。貯蓄の例でいうと、
平均値=1791万円
中央値=1061万円
最頻値=100万円未満
で、比較すると、最頻値を100万円としても、最大で18倍もの違いがあります。これは 「平均値が必ずしも『ふつう』を表わしていない」 ということです。
ケースバイケースなのですが、87ページの図のように、きれいな左右対称の釣鐘型のグラフ(正規分布という、いちばん上のグラフ)の場合は、平均値、中央値、最頻値の3つは、ほぼ一致します。
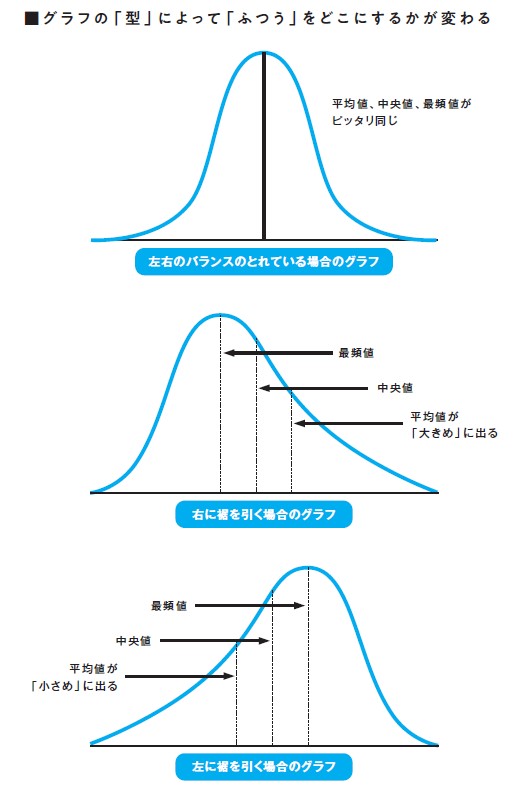
これに対し、右に裾を引いたり(真ん中の図)、左に裾を引くグラフ(いちばん下の図)のケースでは「中央値」が「ふつう」の値として適しているといえます。
では、中央値だけでいいのかというと、少し、心もとなさを感じます。なぜなら、いちばん多い貯蓄は100万円未満の世帯であり、他を圧倒していました。しかも、1061万円の10分1です。
困ってしまいますね。実態を知るにはどうすればよいでしょうか? 会議などの資料として提出するときは、平均値または中央値をメインに据え、参考データとして最頻値を添えるといった使い方をすることが、誤った方向に誘導しない、正直な扱い方だといえます。
代表値はいろいろなタイプがあるよ
ある会社の労働組合では、ボーナスのときは88ページのようなデータを経営陣に提出していました。「要求額」だけだと何の根拠もなく、組合執行部の「希望額」のように見えてしまいます。組合員全体の意見はどうなのか、それを経営陣に示すにはどうするか。
そこで、組合員全員の平均値、中央値、最頻値に加えて、最大値・最小値も正直に追加してまとめていました。
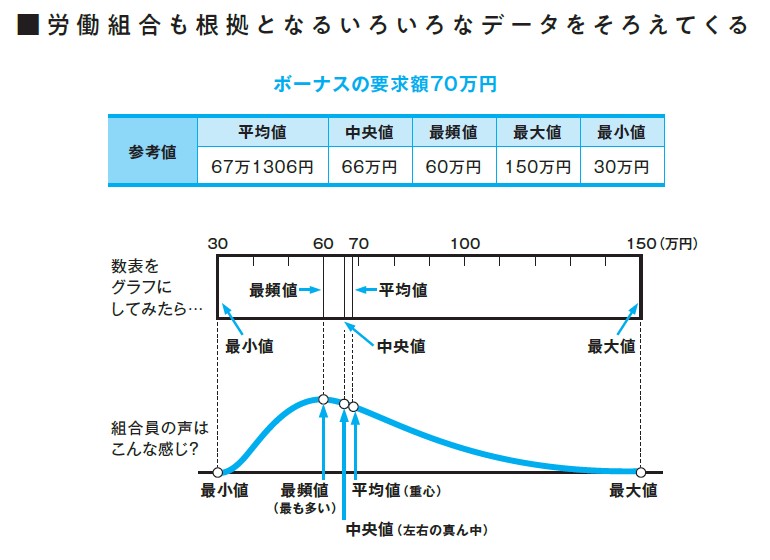
ここまでくると、根拠(エビデンス)のない数字とはいえなくなります。数字を見ていてわかると思いますが、 平均値は端数が出ることが多く、最頻値は切りのよい数字になる傾向があります 。そして最大値・最小値は外れ値になりやすいといえます。
1つの代表値にこだわるより、複数の代表値で補足するほうが現実的といえるでしょう。
