はじめに
機械の不具合を事前に見抜け!
株価の動向、子どもの成長という「生活の中」での統計学の使われ方を見てきましたが、仕事の品質管理にも同じ統計手法が使われています。
株価や子どもの成長にバラツキがあるように、人間が何かモノをつくっても、そこにはバラツキがあります。たとえ最新鋭の機械で製造しても、バラツキは生じます。この バラツキの度合いを数値化したものが、先ほどから述べている「標準偏差」 でした。
次ページの図は、製品のバラツキ具合を示したものです。たとえば、10ミリと指定されたクギの長さが9.998ミリ、10.001ミリのように、製品に超微妙なバラツキが出ると考えてください。
わずかなバラツキで規定内であれば、「合格品」として出荷されるでしょう。
でも、さすがに2ミリも違うクギであれば「不合格品」としてはねられます。
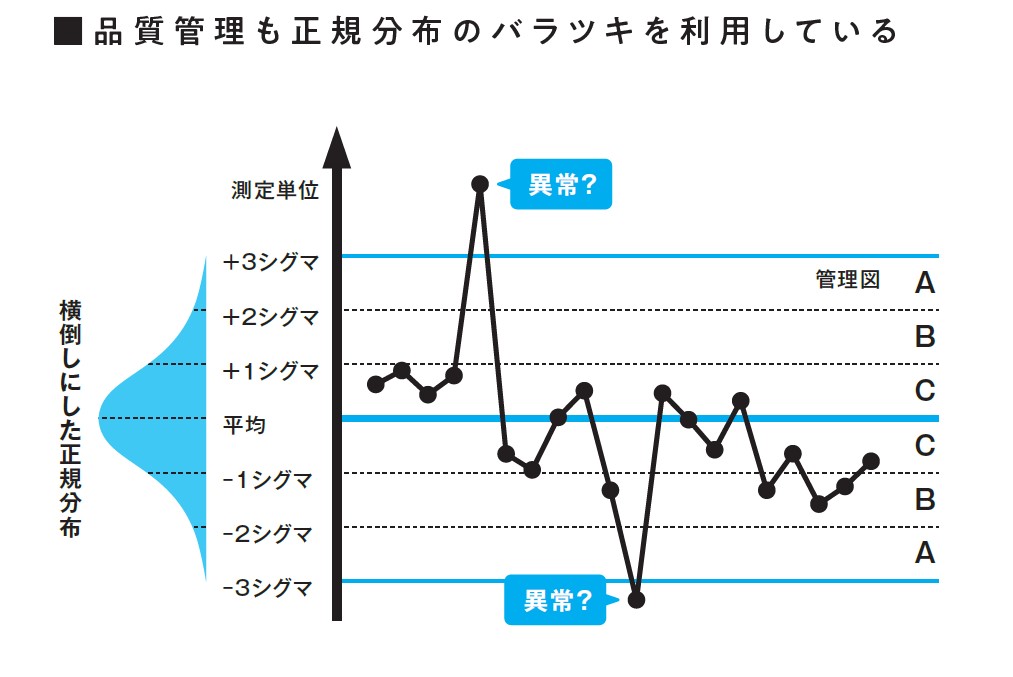
上のグラフは、真ん中の太い青線が平均(標準品)で、その上下にそれぞれC、B、Aの区域があります。これはクギのバラツキ具合を表わしています。
バラついても、クギの約68%が上下のCの範囲に収まり、Bの範囲には約95%のクギが、そしてAの範囲内には99.7%のクギが収まります(この%は統計学でわかっています)。
前もって「機械の故障」が予測できる
このC、B、Aの範囲は、先ほどの「標準偏差」のレベル(1~3)を表わしていて、その外側へ飛び出すクギは稀ま れにしか出ないことを示し、おそらく、そのクギは不合格品(オシャカ)としてはねられてしまうことでしょう。
はねられないにしても、いちばん外側のAの枠に入る製品が3個も続けてつくられるとか、同じ側(上や下)で連続して9個も10個も出てくるとなると、機械の不具合や手順などにトラブルが生じ始めたことを示す〝 予兆 〞かもしれません。
そこで、 製品としては正常内のバラツキだとしても、このA~Cに入る個数が連続するようであれば、統計学の知識を利用し、「いったん機械を止め、検査してみよう」という判断に使うことができます。
実際、日本JIS規格では次ページの表のように、「目安」(ガイドライン)を決めています。これは業界やメーカー、製品によっても異なるのであくまでも目安にすぎませんが、バラツキ(標準偏差)を見て、機械の調子を判断しているのです。

品質管理でも正規分布曲線を横倒しに使っていることがわかりました。統計学を学んでいても、90度横倒しにしたボリンジャーバンドや品質管理グラフを見る機会はほとんどなく、同じものと気づかないかもしれません。
なお、ボリンジャーバンド、成長曲線、品質管理などの指標やグラフは「絶対に正しい」というわけではありませんが、統計学的に見て、リスクのレベルやその目安をあなたに教えてくれているのです。
統計学の素養を身につけていると、ビジネスで失敗を避けるチカラがつきますよ。
